Analise de Regressão

Video sobre a Ferramenta

Definição (O que?)

A análise de regressão é uma ferramenta padrão utilizada na engenharia para analisar dados de experimentos, onde aplicam técnicas e lógicas matemáticas para relacionar as variáveis. Identifica quais variáveis têm maior impacto diante de um tema de interesse. E prevê valores às variáveis dependentes, assumindo valores para as variáveis independentes.

Utilidade (Para que?)

• A regressão linear pode ser aplicada a diversas áreas de estudo empresarial e acadêmico.
• Gerar previsões para evitar desperdícios.
• Identificar uma função que apresente uma relação entre a variável dependente e a variável independente, onde seja possível presumir qual o valor que a assumirá a variável dependente.
• Fornecer insights que podem antecipar os momentos nos quais os produtos de uma empresa estarão com alta demanda

Procedimentos (Como?)

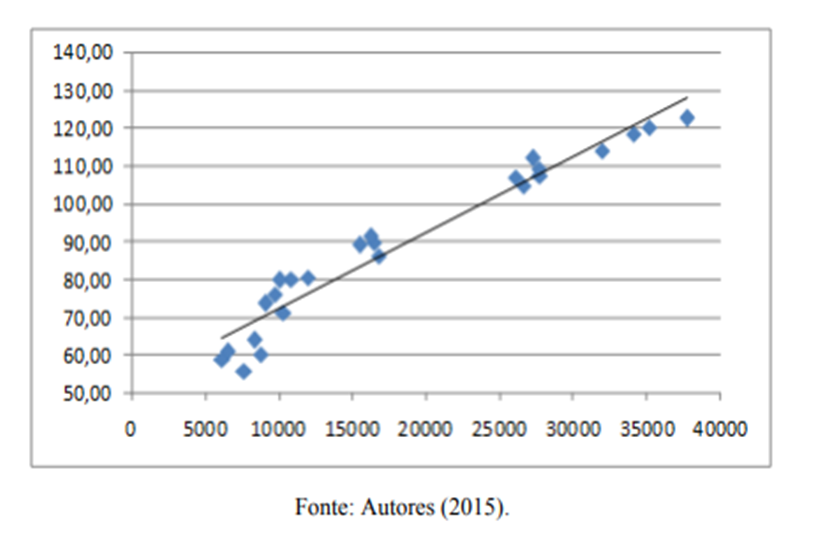
Neste modelo é considerado um preditor X e uma variável dependente ou uma resposta Y. Imagine que a relação verdadeira entre Y e X é uma linha reta e que a observação Y em cada nível X é uma variável aleatória.

•A análisede regressão linear simples é responsável por avaliar a relação  linear entre duas variáveis, sendo uma resposta e uma explicativa (um preditor).
•As variáveis dependentes são as mais importantes, são aquelas que tentamos prever, enquanto as variáveis independentes são aqueles fatores que podem afetar a variável dependente.
•Dentro da ferramenta Análise de Regressão existe o Modelo de Regressão Linear Múltipla.
•Consiste em um método utilizado quando há uma variável dependente e uma ou mais variáveis independentes. Esse método descreve uma função que aborde um resultado aproximado para a variável dependente a partir dos valores das variáveis independentes.
•O contexto básico da regressão linear múltipla é quando a variável Y é de difícil mensuração, e que se necessita de várias variáveis para que se possa encontrar o resultado da variável Y, onde os passos para a realização da análise são a seleção de uma lista das possíveis variáveis X, a coleta de dados das variáveis selecionadas, a verificação das relações entre as variáveis X e Y, podendo eliminar as que não possuem uma boa relação e verificar redundâncias nas variáveis X.

Áreas de aplicação

• Permite determinar o grau em que as variáveis independentes influenciam as variáveis dependentes.
• Além disso, permite explicar um fenômeno e prever coisas sobre o futuro, assim como também pode obter informações comerciais valiosas e acionáveis.
• Este método oferece informações sobre a organização dos custos e como as funções das variáveis podem afetar o produto.
• Auxilia no desenvolvimento de estratégias para melhorar a qualidade de seus produtos e serviços.

Fonte/Referências

• “Avaliação a partir da Análise de Regressão da Influência de Parâmetros Meteorológicos da Poluição Atmosférica de MP-10 em um ponto de Belo Horizonte” da Associação Brasileira de Engenharia de Produção (ABEPRO)

© Copyright 2022. UFF - Todos os direitos reservados.