Análise de Variância

Video sobre a Ferramenta

Definição (O que?)

A análise de variância (ANOVA) é uma técnica de análise estatística padrão, que pode ser utilizada para analisar o erro de medição e outras fontes de variabilidade, perante os dados de um estudo de sistemas de medição. No método ANOVA, a variação pode ser decomposta em quatro categorias: peças, avaliadores, interação entre as peças e avaliadores e erro de replicação.

Utilidade (Para que?)

• Conduzir estudos que seja necessário comparar mais que um fator com relação a uma ou mais respostas;
• Identificar a variabilidade originada pelo erro de operação, instrumento ou produto;

• Avaliar se há uma diferença significativa entre os elementos avaliados;

Procedimentos (Como?)

Para calcular essa a variância, é necessário calcular o quão distante cada observação está em relação ao grupo.

Cálculos da Análise de Variância

• Após isso, é feito os cálculos de MQP, MQO, MQPO e MQE, que, respectivamente, significa a média quadrática para a parte fatorial, média quadrática para o fator operador, a média quadrática para o termo de interação e a média quadrática para o termo do erro.

Áreas de aplicação

• Em sistemas que são necessários avaliar a variância de duas ou mais amostras, para que assim seja calculada a média e determinado se há uma diferença significativa entre elas;

Exemplo

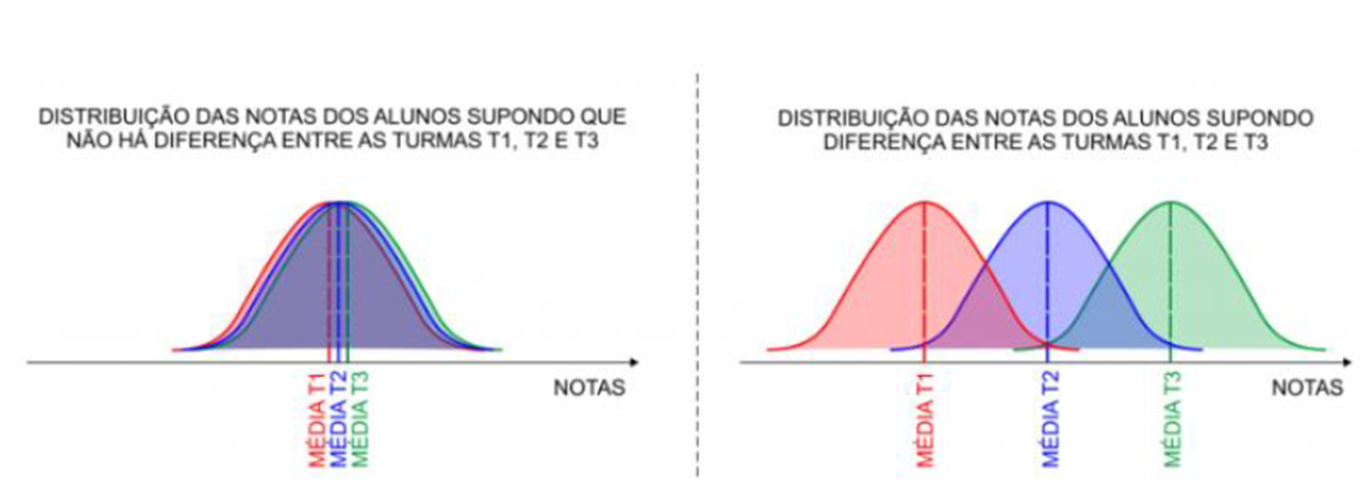
Um dos objetivos da aplicação da ANOVA é realizar o teste estatístico para verificar se há diferença entre distribuição de uma medida entre três ou mais grupos. Em nosso exemplo, podemos definir as hipóteses do teste como:

H0: Não existe diferença entre o desempenho das notas dos alunos de cada professor.

H1: Há pelo menos um professor com alunos com desempenho diferente.

Caso os três grupos de alunos apresentem mesma variabilidade e a mesma média de desempenho, suas distribuições tendem a se sobrepor, confirmando a hipótese de que não existe diferença entre o desempenho das notas dos alunos de cada professor. Caso contrário, quando os grupos apresentam a mesma variabilidade interna e médias de desempenho diferentes, as distribuições se distanciam quanto mais as médias de desempenho se diferenciam

Para aplicação da análise de variância, são necessárias algumas suposições, sendo elas:

As observações são independentes, ou seja, cada elemento amostral (aluno) deve ser independente;

Os grupos comparados apresentam a mesma variância;

Os erros são independentes e provenientes de uma distribuição normal com média igual a zero e variância constante.

Cabe ressaltar que os grupos de alunos de cada professor podem ser vistos como três níveis de um mesmo fator, sendo que o objetivo é saber se o fator professor exerce alguma influência na variação do desempenho das notas de matemática.

As informações geradas na análise de variância estão resumidas na tabela abaixo. Nela são apresentados os graus de liberdade, a soma de quadrados, o quadrado médio, a estatística F e o valor-p.

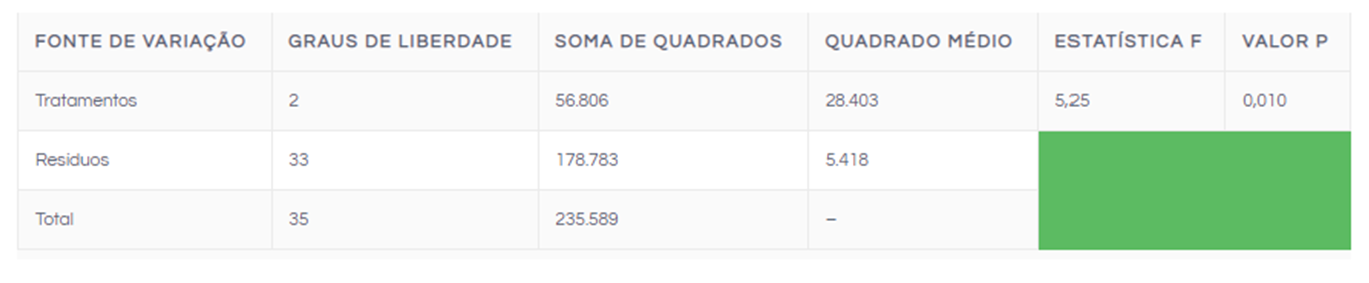
Os graus de liberdade são calculados com base no número de professores (grupos) e no número total de alunos.

A soma de quadrados mede a variação dos dados. A soma de quadrados total mede a variação total nos dados, a soma de quadrados dos tratamentos mede a variação entre os professores de cada turma e a soma dos quadrados dos resíduos mede a variação dentro de cada turma, ou seja, mede a variação dos alunos de cada professor.

O quadrado médio é a razão entre a soma de quadrados e os graus de liberdade e a estatística F, pode ser encontrada na tabela de distribuição F de Fisher-Snedecor.

Como interpretar os resultados da ANOVA?

Tomando como base a tabela anterior, pode-se concluir que existe pelo menos dois professores com alunos com desempenho significativamente diferentes ao avaliar o valor-p = 0,010 (menor que o nível de significância estabelecido de 0,05).

A conclusão da ANOVA pode ser feita também com base na Estatística F. A estatística F tem distribuição F de Fisher-Snedecorcom k-1 e n-k graus de liberdade, onde k é o número de grupos (k = 3) e n é o número de observações (n = 36). Neste caso fictício, obteríamos F ≅3,32 e como a Estatística F (5,25) foi maior que o F tabelado (3,32), conclui-se que existe pelo menos dois professores com alunos com desempenho significativamente diferentes.

Fonte/Referências

• “Avaliação do erro de medição obtido por visão computacional de um processo de soldagem de revestimento de chapas de aço ABNT1020”

© Copyright 2022. UFF - Todos os direitos reservados.