BoxPlot

Video sobre a Ferramenta

Definição (O que?)

O Box plot é um gráfico que sumariza a análise exploratória de dados. Dessa forma, o box plot é um recurso visual que resume os dados para exibir a mediana, quartis e os valores pontuais máximos e mínimos. Portanto, apresenta valores de tendência central, dispersão e simetria dos dados agrupados.

O Box plot é um tipo de gráfico usado regularmente na pesquisa científica e a sua construção é possível por meio de diversos softwares estatísticos.

Utilidade (Para que?)

O box plot pode ser utilizado visando a aplicação e interpretação dos dados quantitativos quando bem indicado. Em determinados casos o Box plot é um substituto aperfeiçoado para as tabelas.

Procedimentos (Como?)

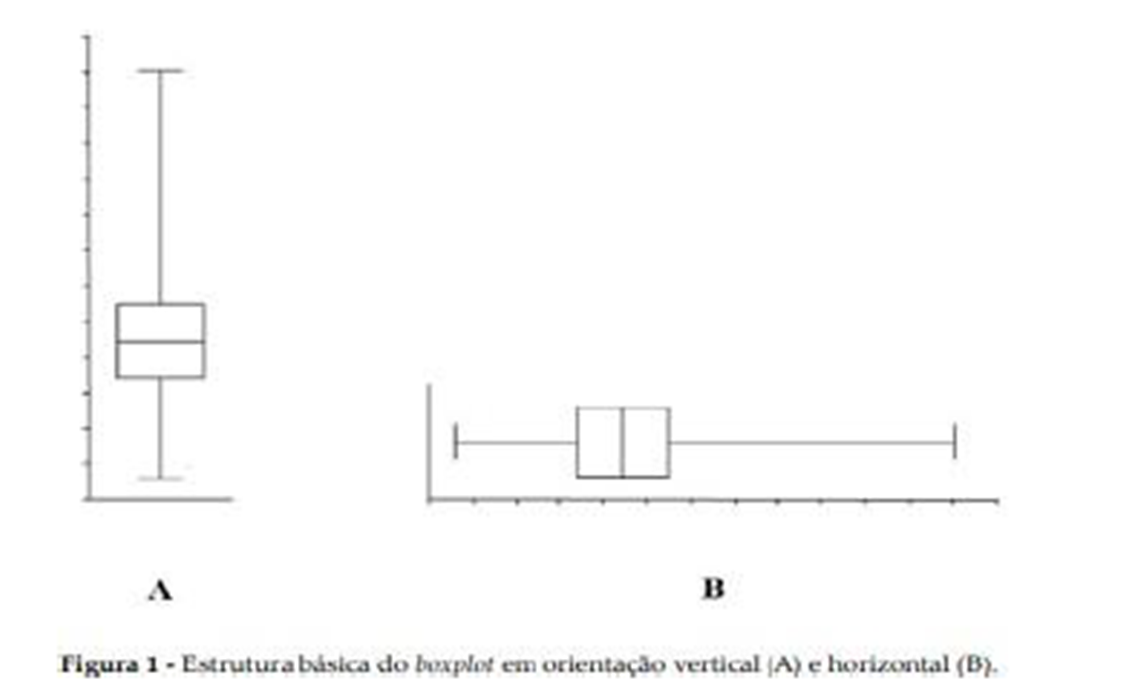
O boxplot pode ser configurado em orientação horizontal ou vertical, ambas com o formato de “caixa e haste” (Figura1). A estrutura básica é constituída por:

a. Caixa (box), que assume comumente o formato retangular;

b. Mediana (desenhada como uma linha dentro da caixa e simbolizada por Q2, ouseja, segundo quartil). Caso haja a representação de um conjunto de dados com distribuição normal, a linha é desenhada no centro da caixa, simbolizando a aproximação com a média aritmética;

c. Haste (bigode ou whisker), assemelhando-se à letra“T”, representativa dos valores compreendidos entre a caixa e os valores limites, inferior e superior, do conjunto de dados. A extremidade da haste é comumente denominada fence.

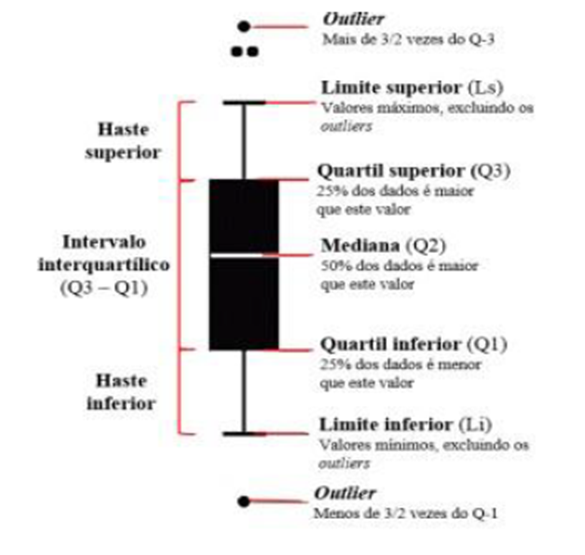
O boxplot exibe a tendência central não – paramétrica (mediana), dispersão (quartis 25% e 75%), forma de distribuição ou simetria da amostra (valores pontuais mínimo e máximo), valores atípicos (outliers) e extremos. Partindo de um boxplot com disposição vertical, têm-se as seguintes informações 5 (Figura2):

a. Eixo vertical: representa dados de valores numéricos;

b. Eixo horizontal: fator de interesse;

c. Primeiro quartil (Q1): onde se localiza ¼ou 25% dos menores valores. Também chamado de quartil inferior ou 25º percentil. Representado pela linha limite inferior da caixa;

d. Mediana ou segundo quartil (Q2): é o local onde ocorre a divisão da metade superior (ou 50%) da metade inferior da amostra. É o 50º percentil. Representada pela linha dentro da caixa;

e. Terceiro quartil (Q3): onde se localiza ¾ ou 75% dos valores maiores. Também chamado de quartil superior ou 75º percentil. Representado pela linha limite superior da caixa;

f. Intervalo interquartílico (Q3-Q1ou IIQ): é definida como a diferença entre Q3 e Q1. No gráfico é representado pela dimensão da caixa. Estende-se do Q1 ao Q3 (percentis 25º a 75º). Representa o intervalo dos 50% dos dados em torno da mediana;

g. Limite inferior (tamanho ou extremidade do whisker ou fence inferior): valor mínimo do conjunto de dados,até1,5 vezes o IIQ (uma vez e meia o intervalo interquartílico), excluindo os outliers e/ou extremos;

h. Limite superior (tamanho ou extremidade do whisker ou fence superior): valor máximo do conjunto de dados, até 1,5 vezes o IIQ (uma vez e meia o intervalo interquartílico), excluindo os outliers e/ou extremos;

i. Outliers (valores atípicos): valores acima e/ou abaixo de 1,5 vezes o IIQ;

j. Extremos: valores acima e/ou abaixo de 2,5 vezeso IIQ (duas vezes e meia o intervalo interquartílico) 6.

Área de aplicação-Exemplo

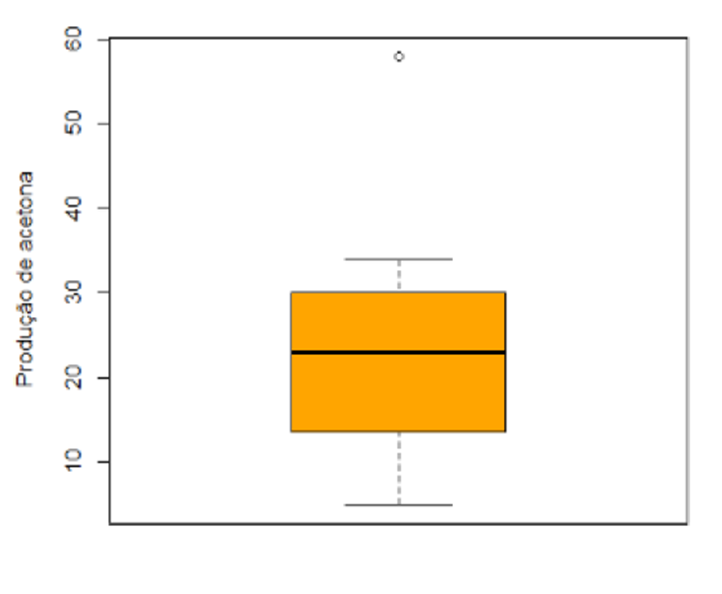
Exemplo: Um engenheiro em uma indústria química é responsável pela produção de acetona. Para avaliar a linha de produção, o gerente monitora o processo. Durante uma semana, 16 bateladas de acetona são produzidas e uma leitura por batelada é feita. Os resultados são apresentados na tabela abaixo.

Arrumamos os dados em ordem crescente: 5, 6, 11, 12, 15, 17, 19, 22, 24, 25, 28, 29, 31, 32, 34, 58

Desses dados calculamos os quartis, a mediana a distância entre quartis, o mínimo e o máximo:

Q1=13.5          M=23           Min=5

IQR=16.5        Q3=30          Max=58

O Boxplot é apresentado a seguir.

Fonte/Referências

NETO, José Valladares e tal. Boxplot: um recurso gráfico para a análise e interpretação de dados quantitativos. Revista Odontológica do Brasil Central, v.26, n. 76, 2017.

PETENATE, Marcelo. BoxPlot: Saiba tudo sobre o Diagrama de caixa e como interpretar esse gráfico. Escola edti. Disponível em: https://www.escolaedti.com.br/o-que-e-um-box-plot Acesso em: 09, junho de 2022.

© Copyright 2022. UFF - Todos os direitos reservados.